Glossary
absolute approach to complexity. According to the absolute approach to linguistic complexity, a language system is more complex the more parts it has, where ‘parts’ can be construed in any of a variety of ways; in this approach, complexity is regarded as an inherent and objectively measurable property of language systems. Opposite of relative approach to complexity. (See Miestamo 2008.) [§11.1]
accidental. Where lexeme L belongs to IC A and is an impostor relative to IC B, L is an accidental impostor if (i) only a small number of L’s realized cells make it appear to be a member of B and (ii) the members of A are not in general impostors relative to B. Opposite of essential. [§6.1]
adaptive. In an adaptive principal-part scheme for an IC system, each lexeme has an ordered sequence of principal parts in which the exponence of the lexeme’s nth principal part determines the MPS of the (n + 1)th principal part. [§1.3.2]
adequate. An adequate principal-part set for lexeme L is any set of cells in L’s realized paradigm that uniquely determines all of the other realized cells in that paradigm (that is, one that uniquely determines L’s IC membership). [§1.3.2]
amassed. An amassed IC includes more than one lexeme. Opposite of singleton. [§8.4]
annexation hypothesis. Different parts of a heteroclite lexeme’s realized paradigm belong to different ICs. See also autonomy hypothesis. [§6.2]
autonomy hypothesis. A heteroclite lexeme belongs to an independent IC whose exponences happen to resemble those of other ICs. See also annexation hypothesis. [§6.2]
broadly belong. A lexeme belonging to any IC J broadly belongs to every proper superclass of J. See also narrowly belong. [§9.3.1]
cell. A cell in the paradigm of lexeme L is the pairing áL, σñ of L with a complete and coherent MPS σ for which L is inflectable. See also realized cell. [§1.1]
cell predictability. Intuitively, the cell predictability of a cell áw, σñ in a lexeme L’s realized paradigm PL is the ratio of (a) to (b), where (a) is the number of nonempty subsets of PL’s cells whose realization uniquely determines áw, σñ and (b) is the number of all nonempty subsets of PL’s cells. Cell predictability is measured by the following formula; see §4.6 for details.
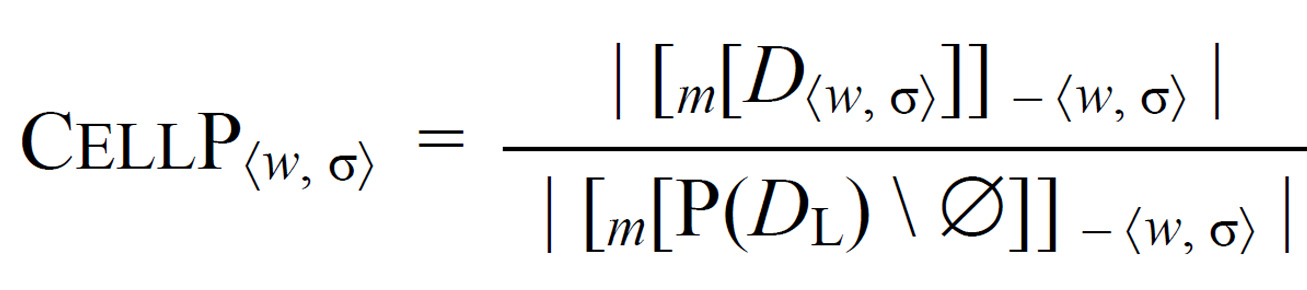
cell predictor number. Where P is the realized paradigm of a lexeme belonging to IC J, J’s cell predictor number is the number of dynamic principal parts required to determine a cell in P, averaged across the distillations in P. [§3.3]
central. A central IC has relatively many members. Opposite of marginal. [§8.1]
complexity. The complexity of an IC system is the extent to which it inhibits motivated inferences about a given lexeme’s realized paradigm from subsets of that paradigm’s cells. [§1.2.2]
condensed. In a condensed IC system, a realized paradigm’s least predictable cells tend to realize the same group of MPSs from one IC to another. Opposite of diffuse. [§4.8]
conditional entropy. The measure of conditional entropy applies to items that have multiple components. The first component M1 might make it easier to establish the value of the second component M2. In that case, the conditional entropy of M2 given the value of M1 is less than the entropy of M2 alone. The formula for conditional entropy is
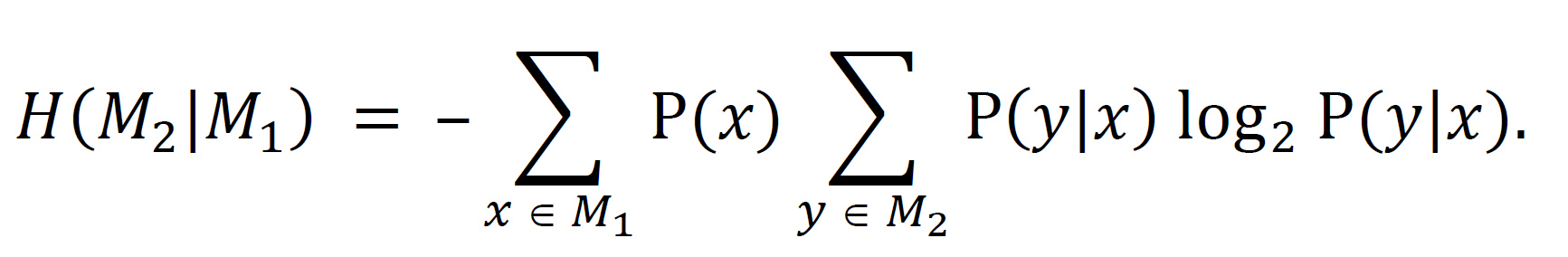

See also entropy. [§10.1]
deductive function. The deductive function of a lexeme L’s principal parts is their use in inferring L’s other realizations. See also matching function. [§6.1]
density. The density of an IC system’s static principal-part sets is the ratio of actual to possible optimal static principal-part sets, given the system’s number of distillations and the size of its optimal static principal-part sets. [§11.3.2]
depth-of-inference contrast. Languages vary widely in the number of dynamic principal parts they require to distinguish a given IC, but they show a high degree of uniformity in allowing a given form in a lexeme’s paradigm to be deduced from a low number of dynamic principal parts (the average number being not much more than one). [§7.7]
diffuse. In a diffuse IC system, a realized paradigm’s least predictable cells do not invariably realize the same MPSs across different ICs, but are dispersed in different ways in different ICs. Opposite of condensed. [§4.8]
distillation. Where S is a set of MPSs whose exponences in some IC system are isomorphic, the distillation of S is a member of S chosen to represent all members of S; typically, the distillation of S is the first member of S on some specified ordering of its members. [§2.1.1]
distinguisher. The substring by which a word form is distinguished from all distinct word forms in its realized paradigm is its distinguisher; for instance, ought is the distinguisher of bring’s past-tense form brought. See also theme. [§2.1.2]
dynamic principal-part number. A lexeme’s dynamic principal-part number is its number of dynamic principal parts on any optimal analysis. An IC’s dynamic principal-part number is that of its member lexemes. An IC system’s dynamic principal-part number is the average of its member ICs’ dynamic principal-part numbers. [§3.2]
dynamic. In a dynamic principal-part scheme for an IC system, the optimal principal-part sets of lexemes belonging to distinct ICs may differ in number and needn’t realize any of the same MPSs. [§1.3.2]
entropy. The entropy of a set C of items is a measure of variation in C, calculated by
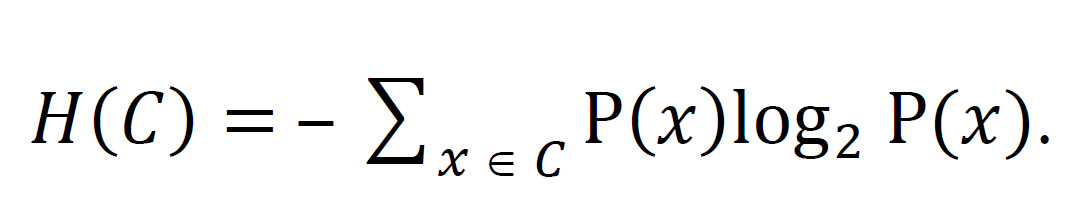

See also conditional entropy. [§10.1]
essential. Where lexeme L belongs to IC A and is an impostor relative to IC B, L is an essential impostor if (i) all members A are impostors relative to B and (ii) there are pervasive inflectional similarities between A and B. Opposite of accidental. [§6.1]
exponence. The exponence of an MPS in some word form is the full set of exponents of that property set in that word form. Contrast exponent; see also rule of exponence. [§1.2.2]
exponent. An exponent is a minimal morphological realization of some morphosyntactic property or MPS; it is minimal in the sense that no proper subpart of it is itself an exponent. Contrast exponence. [§1.2.2]
formative-based approach. In the formative-based approach to principal-part analysis, the exponence of a given MPS or indexed stem is invariably a morphological formative (or the significative absence thereof). Opposite of stem-referral approach. [§7.8]
global complexity. In language typology, global complexity refers to the complexity of an entire language. Opposite of local complexity. (See Miestamo 2008.) [§11.1]
hearer-oriented. In a hearer-oriented plat, an IC system’s exponences are represented as audible phonological distinctions, either in full phonetic detail or with the effects of automatic phonology factored out. Contrast speaker-oriented. [§2.2]
heteroclite. A heteroclite lexeme’s paradigm inflects partly according to the pattern of one IC and partly according to the pattern of another. [§6.2]
IC. See inflection class.
IC diacritic. In the lexicon, an IC diacritic specifies a lexeme’s IC membership by naming the IC to which L narrowly belongs. [§1.2.1]
IC identifier. An IC identifier is a cell that is a predictor of every other cell in a lexeme L’s realized paradigm (that is, one that uniquely determines L’s IC membership). [§5.2.5]
IC-MPS entropy. Given an IC J and a distillation M in a reduced plat, the IC-MPS entropy HJ,M is an average of the entropies of all other MPSs M′ conditional on M, calculated as
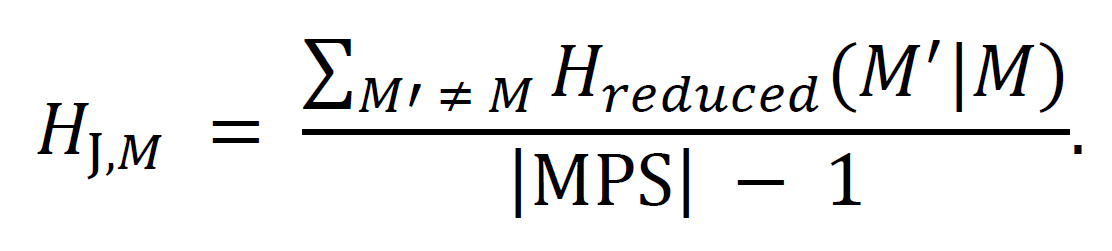

[§10.5]
IC predictability. Intuitively, the IC predictability of a lexeme L’s IC is the fraction of adequate (though not necessarily optimal) dynamic principal-part sets among all nonempty subsets of cells in L’s realized paradigm. The IC predictability of a lexeme L’s IC is measured by the following formula; see §4.4 for details.
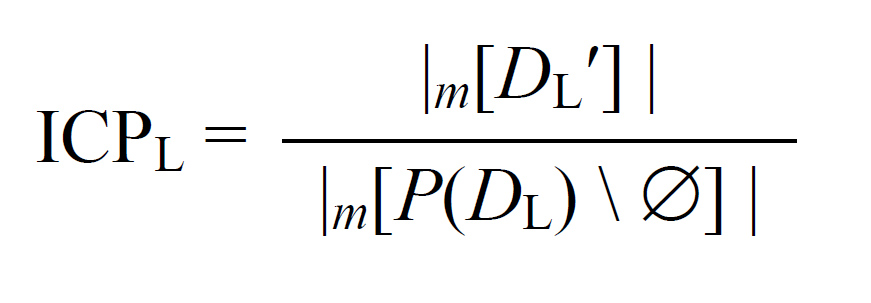
IC predictable entropy (ICBE). Where J is an IC, n-ICBEJ is the component of the n-MPS entropy due to the exponence of J, averaged across all MPSs. This is calculated as
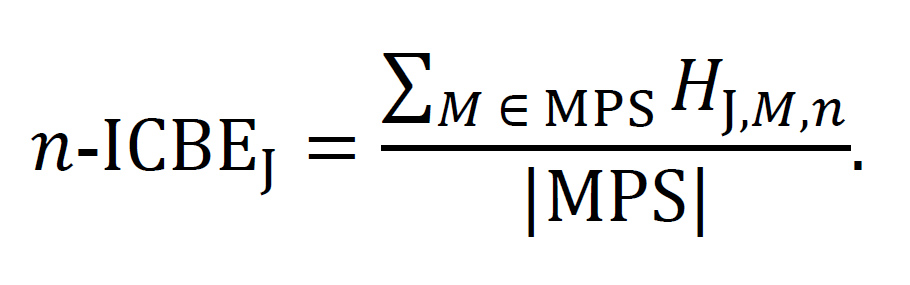

[§10.5]
IC predictive entropy (ICVE). In a reduced plat, the ICVEJ is the average of the IC-MPS entropies HJ,M over all MPSs M in the reduced plat:
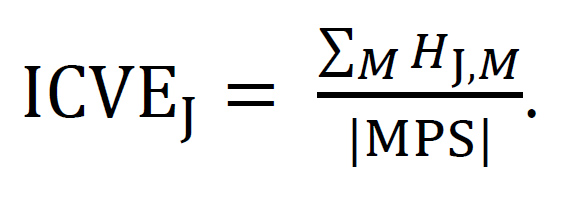
 .
.
[§10.5]
IC system. An IC system for a syntactic category C is a set S of ICs such that every lexeme belonging to C belongs to some IC in S. [§1.1]
IC transparency. The IC transparency of an IC J is a function of the implicative relations exhibited by the realized paradigms of L’s members: the more implicative relations they embody, the greater J’s paradigmatic transparency. In the realized paradigms of lexemes belonging to a maximally transparent IC, each cell’s exponence determines that of every other cell; given any two cells K1, K2 in a realized paradigm belonging to an IC of this sort, there an R-relation deducing K1 from K2. By contrast, in the realized paradigms of lexeme’s belonging to a maximally opaque IC, no cell or combination of cells determines the exponence of any other cell; in a realized paradigm belonging to an IC of this sort, there are no R-relations deducing any cell from any other cell or combination of cells. [§4.1]
implicative relation. An implicative relation among the cells of a lexeme’s realized paradigm is a relation of the type “the realized cells áw1, σ1ñ, …, áwn, σnñ determine the realized cell áx, τñ”. [§1.1] See W-relation, R-relation.
implicative rule. An implicative rule is a realization rule that expresses an implicative relation among cells of a realized paradigm. [§1.2.1]
impostor. An impostor is a lexeme whose inflection-class membership is ambiguous because one or more of its realizations is morphologically ambiguous. Example: the verb speed’s realization speed is ambiguous, since it could reflect membership in the conjugation class of feed (past tense fed) on in that of need (past tense needed). [§6.1]
indexed stem. An indexed stem is a stem whose distribution is determined by its association with a morphological index that has no necessary correspondence to the stem’s form or to the MPS(s) that it is used to express. [§7.1]
inflection class (abbreviation: IC). An inflection class is a class J of lexemes such that (i) J’s members are distinguished by a common pattern of inflection and (ii) membership in J has no syntactic significance. Conjugation classes and declension classes are ICs. [§1.1]
irreducible. See reducible.
isomorphic ideal. The isomorphic ideal is the property attained by an IC system in which each MPS’s pattern of exponences across ICs is isomorphic to that of every other MPS (so that all MPSs belong to the same distillation). [§8.6]
local complexity. In language typology, local complexity refers to the complexity of a particular linguistic subsystem. Opposite of global complexity. (See Miestamo 2008.) [§11.1]
lookahead heuristic. The lookahead heuristic is a way to find static near-principal parts: start with an empty S and repeatedly add the most predictive remaining MPSs to it until the residual entropy of the remaining MPSs is small enough. Compare simple heuristic. [§10.4]
Marginal Detraction Hypothesis. Marginal ICs tend to detract most strongly from the IC predictability of other ICs. [§8.1]
marginal. A marginal IC has relatively few members. Opposite of central. [§8.1]
matching function. The matching function of a known lexeme’s principal-part set S is the use of S in inferring the IC membership of an unfamiliar lexeme whose inflection matches S. See also deductive function. [§6.1]
maximally opaque IC. See IC transparency.
maximally transparent IC. See IC transparency.
minimal. An adequate set of principal parts is minimal if none of its proper subsets is adequate. [§1.3.2]
morphosyntactic focus number. An IC system’s morphosyntactic focus number is a measure of its degree of morphosyntactic focus. It is measured as 1 ‒ (i/(j × k)), where i is the number of distinct distillations realized by optimal static principal parts, j is the number of optimal static principal-part sets, and k is the number of members in each set. See also morphosyntactically focused, morphosyntactically unfocused. [§3.4]
morphosyntactic property. A morphosyntactic property is the specification of an inflectional category by one of its permissible values. Example: the morphosyntactic property ‘number:singular’ is a specification of the inflectional category of number. Where there is no risk of ambiguity, we abbreviate the morphosyntactic property C:v (where C is an inflectional category and v is one of C’s permissible values) as v. [§1.1]
morphosyntactic property set (abbreviation: MPS). Given a syntactic category C, a morphosyntactic property set for C is a set of morphosyntactic properties appropriate to C. Example: {case:nominative, number:singular, gender:feminine} is a morphosyntactic property set for adjectives in Latin. [§1.1]
morphosyntactically focused. An IC system is morphosyntactically focused to the extent that the distillations realized by its optimal static principal parts are constrained; an IC system that has only one optimal static principal-part set is maximally focused. Opposite of morphosyntactically unfocused. [§3.4]
morphosyntactically unfocused. An IC system is morphosyntactically unfocused to the extent that the distillations realized by a lexeme’s optimal static principal parts are morphosyntactically unconstrained; an IC system in which every distillation is realized by a principal part in one or another optimal static principal-part analysis is maximally unfocused. Opposite of morphosyntactically focused. [§3.4]
motivated inference. If one infers the forms of a lexeme from an adequate set of principal parts, the inferences are motivated. Example: the inference of sings and singing from the principal-part set sing – sang – sung. Opposite of unmotivated inference. [§6.1]
MPS. See morphosyntactic property set.
narrowly belong. A lexeme L belonging to IC J1 narrowly belongs to J1 iff there is no proper subclass J2 of J1 such that (i) L belongs to J2 and (ii) at least one realization rule is defined as applying to members of J2. Contrast broadly belong. [§9.3.1]
near-principal parts. A set of near-principal parts for some realized paradigm P is a set of cells in P that reduces the residual entropy of P’s remaining cells below some threshold. [§10.4]
n-conditional exponence entropy. Where J is an IC and M is a distillation, the n-conditional exponence entropy for M and J is calculated as

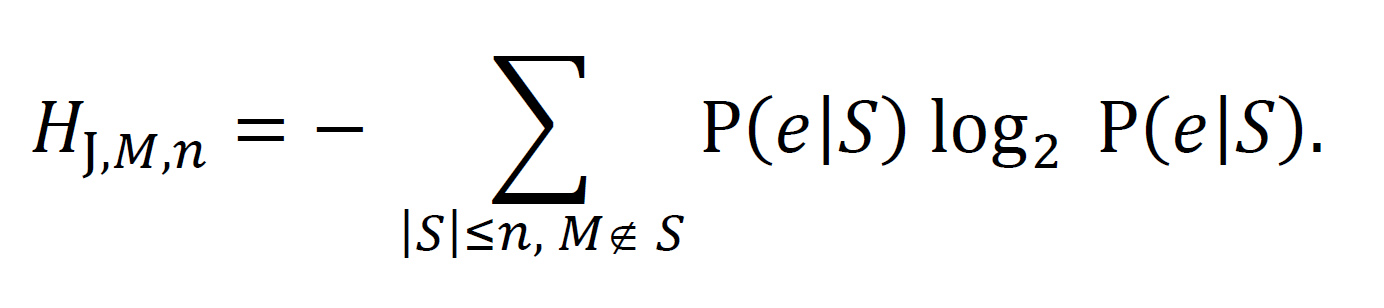
[§10.5]
n-MPS entropy. The n-MPS entropy of an MPS M is the average of the entropy of M conditional on members of CM, the collection of MPSs not including M with up to n members. The formula for n-MPS entropy is
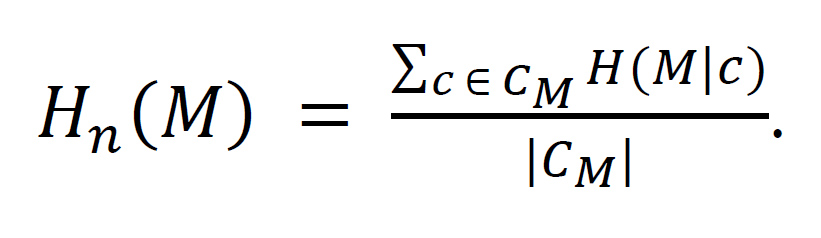
[§10.2]
nonsyncretistic. A relation that allows one cell in a realized paradigm to be determined by another cell in that paradigm is nonsyncretistic if the two cells exhibit different word forms. [§9.2]
optimal set of principal parts. A set S of principal parts (static, adaptive or dynamic) is optimal for IC J if and only if there is no adequate set of principal parts for J whose cardinality is less than that of S. [§1.1]
Pāṇini’s principle. If realization rules R1 and R2 are in competition, R1 is narrower than (and therefore overrides) R2 iff either (a) R1 is defined as applying to a proper subclass of the IC to which R2 is defined as applying, or (b) R1 and R2 are defined as applying to the same IC, but R1 is defined for a smaller number of MPSs than R2. [§9.3.3]
paradigm. The paradigm of a lexeme L is a complete set of cells for L. [§1.1] For maximally transparent paradigm, maximally opaque paradigm, see IC transparency.
paradigm function. A paradigm function is a function from the cells in lexemes’ paradigms to the corresponding cells in their realized paradigms. [§9.3.2]
paradigm schema. A syntactic category’s paradigm schema is the set of MPSs realized by the paradigms of that category’s members. For instance, the paradigm schema of a Latin noun is the set {{nom sg}, {voc sg}, {gen sg}, {dat sg}, {acc sg}, {abl sg}, {loc sg}, {nom pl}, {voc pl}, {gen pl}, {dat pl}, {acc pl}, {abl pl}, {loc pl}}. [§1.1]
plat. A plat is the representation of an IC system as a matrix in which distinct MPSs are represented as columns, distinct ICs are represented as rows, and the exponence of MPS σ in IC J is specified at the intersection of J and σ. [§1.2.2]
plat reduced by J, M. A plat reduced by J, M is a fragment of a plat containing only those ICs that have the same exponence as IC J for MPS M. [§10.5]
predictability. See cell predictability, IC predictability.
predictiveness. The predictiveness of a cell K in a realized paradigm is the fraction of the other cells in the paradigm that are fully determined by K. [§5.2.5]
predictor. Where K1, K2 are cells in a realized paradigm, K1 is a predictor of K2 if K1 fully determines K2. [§5.2.5]
preterite-present. In Germanic languages, preterite-present verbs have (i) present-tense forms exhibiting the morphology usual for Strong verbs in the past tense and (ii) past-tense forms exhibiting the morphology usual for Weak verbs in the past tense. See Weak and Strong. [§8.3]
principal parts. A set of principal parts for a lexeme L is a set of cells in L’s realized paradigm P from which one can reliably deduce the remaining cells in P. If the cell áw, σñ is a principal part, we sometimes refer to the word form w (or to the MPS σ) as a principal part, but with the understanding that we are using w (or σ) as a shorthand for áw, σñ. [§1.1]
pure exponence-based morphology (PEM). According to the PEM hypothesis, the realization rules that define a language’s inflectional morphology include rules of exponence and not implicative rules. Opposite of pure word-and-paradigm morphology. [§9.2]
pure word-and-paradigm morphology (PWPM). The PWPM hypothesis subsumes three axioms: (i) the realization rules that define a language’s inflectional morphology are purely implicative rules; (ii) the stored principal part hypothesis (q. v.); (iii) because a lexeme’s IC membership is determined by its principal-part set, neither IC diacritics nor inflectional stems are stored in the mental lexicon, nor do they figure in the formulation of realization rules. Opposite of pure exponence-based morphology. [§1.2.1]
realization. Where áL, σñ is a cell in the paradigm of lexeme L, áL, σñ is expressed morphologically as a word form w; w is in this context the realization of L, of σ and of áL, σñ. If w realizes áL, σñ, we also sometimes refer to the realized cell áw, σñ as a realization áL, σñ. [§1.1]
realized cell. Where the cell áL, σñ in the paradigm of lexeme L has realization w, L has áw, σñ as a realized cell. [§1.1]
realized paradigm. A lexeme’s realized paradigm is its complete set of realized cells. [§1.1]
reducible. Where S1 → S2 is a valid W- or R-relation, S1 → S2 is reducible iff either (i) there is a proper subset S′ of S1 such that S′ → S2 is a valid relation or (ii) S2 is not a singleton set; otherwise, S1 → S2 is irreducible. [§4.1]
relative approach to complexity. According to the relative approach to linguistic complexity, a language system is more complex if it has a higher “cost” for language users. Opposite of the absolute approach to complexity. (See Miestamo 2008.) [§11.1]
root property set. In an adaptive system of principal parts, the root property set is the MPS realized by the first principal part for all ICs. [§1.3.2]
R-relation. An R-relation is an implicative relation among realization rules. See also W-relation. [§4.1]
rule of exponence. Where áL, σñ is a cell in the paradigm of lexeme L and X is a stem of L, a rule of exponence is a realization rule that applies to the pairing áX, σñ to realize σ through the inflection of X. [§1.2.1]
rule of referral. A rule of referral is a realization rule that specifies that two contrasting cells in a paradigm are realized by identical forms. [§9.2]
signature. An IC’s signature is the pattern of syncretism exhibited by its paradigms. In particular, the signature of an IC J with respect to a set S of MPSs is a partition P of S such that (i) for every s Î P, every member of s has the same exponence, and (ii) for all s1, s2 Î P, if s1’s members share exponence E1 and s2’s members share exponence E2, then E1 = E2 iff s1 = s2. [§7.8]
simple heuristic. A simple heuristic for finding static near-principal parts is to start with an empty set S and repeatedly add the MPS with the highest residual entropy to it until the residual entropy of the remaining MPSs is sufficiently small. Compare lookahead heuristic. [§10.4]
singleton. A singleton IC includes only a single lexeme. Opposite of amassed. [§8.4]
speaker-oriented. In a speaker-oriented plat, an IC system’s exponences are represented as contrasts that a language user recognizes as morphologically significant, incorporating morpholexical as well as phonological information. Contrast hearer-oriented. [§2.2]
static principal-part number. A lexeme’s static principal-part number is its number of static principal parts on any optimal analysis. An IC’s static principal-part number is that of its member lexemes. An IC system’s static principal-part number is that of its member ICs. [§3.2]
static. In a static principal-part scheme for an IC system, the same cells function as principal parts in the realized paradigm of every lexeme belonging to a given syntactic category. See also uniform. [§1.3.1]
stem-formation rule. A stem-formation rule is a stem-realization rule that determines the phonological shape of the stem S bearing a particular index if S is not lexically listed. [§9.3.3]
stem-realization rule. A stem-realization rule is one kind of realization rule, either a stem-selection rule or a stem-formation rule. [§9.3.3]
stem-referral approach. In the stem-referral approach to principal-part analysis, the exponence of an indexed stem S is represented either as a stem formative or, to the extent possible, as the index of a distinct indexed stem with which S is syncretized. Opposite of formative-based approach. [§7.8]
stem-referral pattern A stem-referral pattern is a pattern of syncretism between distinct indexed stems. [§12.9]
stem-selection rule. A stem-selection rule indicates the conditions in which a stem with a particular index is used in the definition of a lexeme’s realized paradigm. [§9.3.3]
stored principal part (SPP) hypothesis. A lexeme L’s entry in the mental lexicon includes a set of principal parts for L. Stored principal-part sets may or may not be unique, uniform or optimal. [§1.2.1]
Strong. In Germanic languages, Strong verbs form their past tense by means of ablaut. Opposite of Weak. See also preterite-present. [§8.3]
theme. The theme of a realized paradigm is the invariant substring shared by all word forms in that paradigm; for instance, br is the theme of the paradigm of BRING. See also distinguisher. In some instances, the boundary between a word form’s theme and its distinguisher happens to coincide with a boundary between stem and affix (as in the forms of the verb WALK). [§2.1.2]
thick. A thick paradigm is one in which all principal parts are necessary to determine each cell (under a particular optimal dynamic principal-part analysis). A thick paradigm’s IC is also thick, as is an IC system consisting entirely of thick ICs. Opposite of thin. [§3.3]
thin. A thin paradigm is one in which each cell is determined by a single principal part (under a particular optimal dynamic principal-part analysis). A thin paradigm’s IC is also thin, as is an IC system consisting entirely of thin ICs. Opposite of thick. [§3.3]
token frequency. Where J is an IC, the token frequency of J is the frequency with which members of J appear in a particular corpus. [§10.3]
type frequency. Where J is an IC of lexemes belonging to syntactic category C, the type frequency of J is the ratio of J’s members to the total number of lexemes in C. [§10.3]
uniform set of principal parts. The principal-part sets of a class C of lexemes are uniform if each member of C has the same members of its realized paradigm as its principal-part set. Traditionally, unique principal-part sets (q. v.) are uniform. [§1.1]
unique set of principal parts. In traditional grammar, a lexeme L is assumed to have a unique set of principal parts, in the sense that the label “principal parts” is reserved for one of L’s (potentially multiple) principal-part sets; the identity of L’s unique principal-part set is agreed upon as a matter of convention. Example: By convention, a Latin noun’s unique set of principal parts consists of its nominative singular and genitive singular realizations. [§1.1]
universe. A universe of ICs is a set of ICs with respect to which some calculation is performed; the universe may be the full set of ICs in a system or one of its proper subsets. [§8.1]
unmotivated inference. If one infers that the principal parts of lexeme L1 match those of lexeme L2 because of a perceived similarity between L1 and L2, the inference is unmotivated. Example: the inference of brang and brung from the similarity of bring and ring. Opposite of motivated inference. [§6.1]
unpredictable. A cell K is unpredictable in the paradigm of some lexeme L if and only if no other cell in L’s paradigm has a realization that is informative about K’s realization. [§4.5]
Weak. In Germanic languages, Weak verbs form their past tense by means of a coronal suffix. Opposite of Strong. See also preterite-present. [§8.3]
word-realization rule. A word-realization rule is one kind of realization rule, either a rule of exponence or a rule of referral. [§9.3.4]
W-relation. A W-relation is an implicative relation among cells in the realized paradigm of a specific lexeme. See also R-relation. [§4.1]
